Regularization for Deep Learning

定义：Any modification we make to a learning algorithm that is intended to reduce its generalization error but not its training error.

Parameter Norm Penalties
- $L^2$ Parameter Regularzation
- $L^1$ Regularization
Regularization and Under-Constrained Problems
Dataset Augmentation
Noise Robustness
Multi-Task Learning
Early Stopping

Parameter Norm Penalties

通过限制模型的能力来正则化，通常在目标函数中加入惩罚项 $\Omega(\theta)$: \[ \hat{J}(\theta; X, y) = J(\theta; X, y) + \alpha \Omega(\theta) \] 这样模型在训练的时候不但会减小原来的 $J$ ，也会尽量减小惩罚项 $\Omega$，从而达到防止过拟合的效果。

需要注意的是，在神经网络中只需要正则化网络中的权重（weights），而偏置不需要正则化，一方面是因为相对于权重，偏置很容易被拟合（使用较少的数据），也没有权重重要，权重需要观察两个变量在各种条件下的情况来进行拟合，而偏置只需考虑一个变量，所以不惩罚偏置也不会对过拟合造成多大影响；另一方面是因为如果对偏置业也进行惩罚则容易造成欠拟合。所以之后用 $w$ 表示所有权重，而 $\theta$ 表示全部参数。

$L^2$ Parameter Regularzation

$L^2$ 正则化又叫 weight decay，岭回归（ridge regression）和 Tikhonov regularization。它在目标函数后加上惩罚项 $\Omega(\theta) = \frac{1}{2}||w||^2_2$，这使得权重趋近于向原点方向更新。

我们可以从梯度更新的角度来理解正则化是怎么工作的，为了简化，假设模型里无偏置参数，即 $\theta = w$，所以目标函数如下： \[ \hat{J}(w;X,y) = \frac{\alpha}{2}w^Tw + J(w;X,y) \] 对 $w$ 求梯度： \[ \bigtriangledown_w\hat{J}(w; X, y) = \alpha w+\bigtriangledown_wJ(w; X,y) \] 所以梯度更新公式为： \[ \begin{align} w &\leftarrow w - \epsilon(\alpha w + \bigtriangledown_wJ(w;X,y)) \\ w& \leftarrow (1-\epsilon\alpha)w - \epsilon\bigtriangledown_wJ(w;X,y) \end{align} \] 可以见得，每次更新梯度时都先会按照一定的因子缩小 $w$，然后在执行正常的梯度下降。

这是执行一步梯度下降发生的事情，若在整个 training 期间都执行此规则会发生什么呢？

线性逼近（Linear approximation）

函数 $f(x)$ 在点 $a$ 处的最佳线性逼近 $L_a(x)$ 要满足: $L_a(a) = f(a)$ 且 $L_a'(a) = f'(a)$，这样可以构造出 $L_a(x) = f(a) + f'(a)(x-a)$。

二次逼近（Quadratic approximation）

函数 $f(x)$ 在点 $a$ 处的最佳二次逼近 $Q_a(x)$ 要满足：

$Q_a(a) = f(a)$

$Q_a'(a) = f'(a)$

$Q_a''(a) = f''(a)$

通过这三个条件可以构造出 $Q_a(x) = f(a) + f'(a)(x-a)+\frac{1}{2}f''(a)(x-a)^2$

也可以根据泰勒公式理解，把 $f(x)$ 在 $a$ 点进行泰勒展开，只保留到二阶导。

为了简化问题，我们在最优点 $w^* = \arg\min_wJ(w)$ 用二次逼近（quadratic approximation）拟合原目标函数，得到新的近似目标函数： \[ \hat{J}(w) = J(w^*)+\frac{1}{2}(w-w^*)^TH(w-w*) \] 其中 $H$ 为 $J$ 对 $w$ 的海森矩阵（Hessian matrix），它是由二阶偏导数组成的方阵，若 $w = [w_1, w_2, …, w_n]$，则： \[ H = \begin{bmatrix} \frac{\partial^2J}{\partial w_1^2} & \frac{\partial^2J}{\partial w_1\partial w_2} & \cdots & \frac{\partial^2J}{\partial w_1\partial w_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial^2J}{\partial w_n\partial w_1} & \frac{\partial^2J}{\partial w_n\partial w_2} & \cdots & \frac{\partial^2J}{\partial w_n^2} \end{bmatrix} \] 我们发现上式中没有一阶偏导数，那是因为 $J$ 的一阶导数在最优点 $w^*$ 的值为 $0$，即 $J'(w^*) = 0$。

当 $\hat{J}$ 取得最小值时，它的梯度 \[ \bigtriangledown_w\hat{J}(w) = H(w - w^*) \] 等于 $0$。

为了研究正则化的影响，我们修改上式，加入 weight decay gradient，我们用 $\hat{w}$ 表示正则化后的 $\hat{J}$ 的最小值的位置，可以解得： \[ \alpha\hat{w} + H(\hat{w}-w^*) = 0 \]

\[ (H+\alpha I)\hat{w} = Hw^* \]

\[ \hat{w} = (H+\alpha I)^{-1}Hw^* \]

可以看出，当 $\alpha$ 趋近于 $0$ 时，$\hat{w} \approx w^*$，那当 $\alpha$ 较大时会发生什么呢？

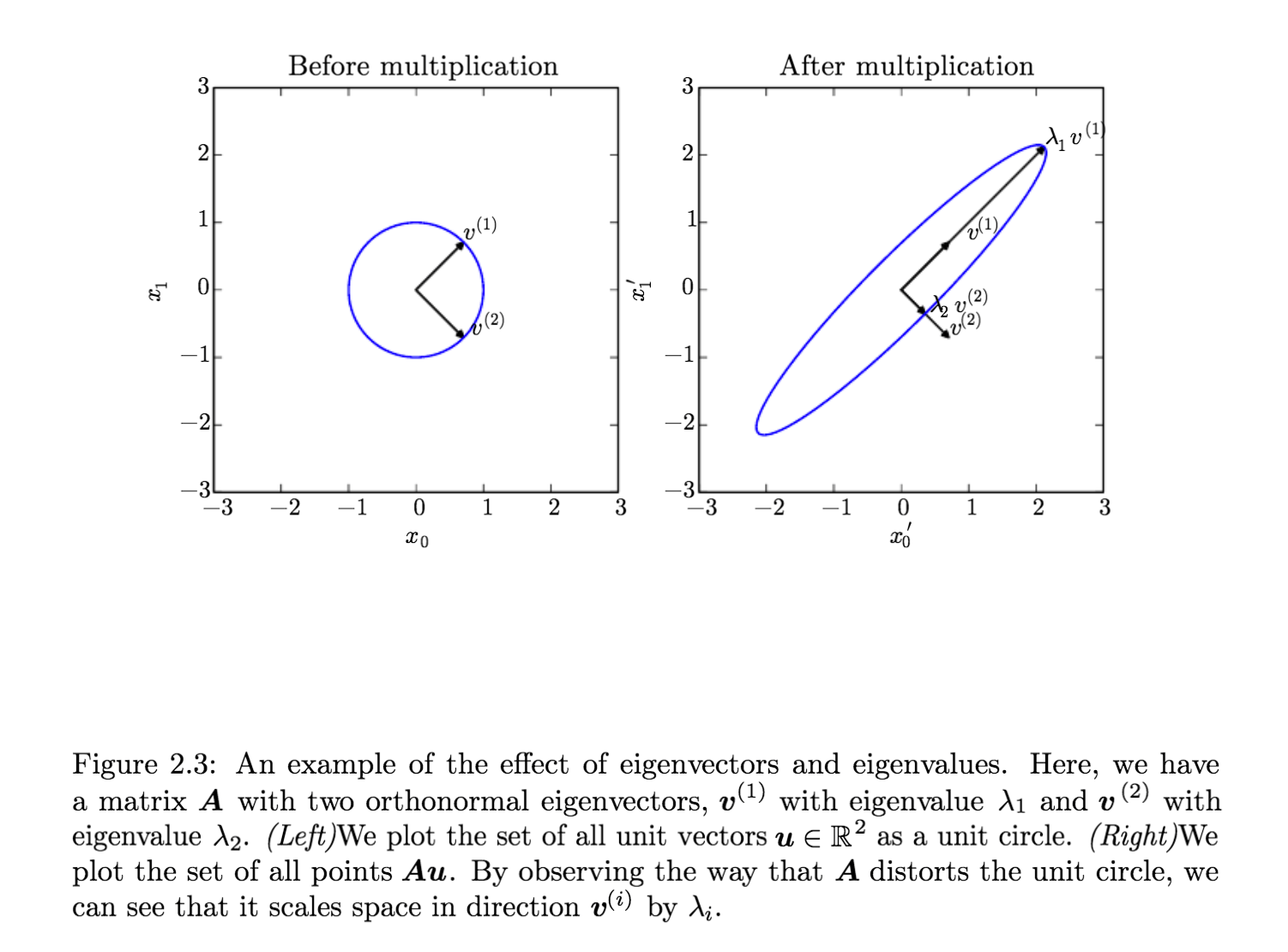
因为 $H$ 由实数组成且对称，所以 $H$ 可以分解为一个对角阵 $\Lambda$ 和正交矩阵 $Q$ 的乘积： \[ H = Q\Lambda Q^T \] 其中，$\Lambda$ 中对角线的元素为 $H$ 的特征值，$Q$ 的每一列为对应的特征向量。

由此可以进一步化简： \[ \begin{align} \hat{w} & = (Q\Lambda Q^T+\alpha I)^{-1}Q\Lambda Q^Tw^* \\ & = [Q(\Lambda+\alpha I)Q^T]^{-1}Q\Lambda Q^T w^* \\ & = (Q^{T})^{-1}(\Lambda+\alpha I)^{-1}Q^{-1}Q\Lambda Q^T w^* \\ & = Q(\Lambda+\alpha I)^{-1}\Lambda Q^T w^* \\ \end{align} \] 令 $ =Q(+I)^{-1}QT $，则 $\hat{H}$ 的任意特征值 $\hat{\lambda_i}$ 与 $H$ 里对应的特征值 $\lambda_i$ 有如下关系： \[ \hat{\lambda_i} = \frac{\lambda_i}{\lambda_i+\alpha} \] 所以 $L^2$ 正则化的效果就是把 $w^*$ 沿着 $H$ (或 $\hat{H}$) 的特征向量所定义的方向重新调整大小（rescale）。其中，$w^*$ 中沿着 $H$ 的第 $i$ 个特征向量方向的成分被扩大了 $\frac{\lambda_i}{\lambda_i+\alpha}$ 倍。

那些大特征值对应的特征向量的方向，$\lambda_i\gg \alpha$，正则化的效果很小；而那些小特征值对应的方向，$\lambda_i \ll \alpha$，$w^*$ 相应方向的成分就很容易缩小到 $0$，正则化效果很明显。

得出后面的结论还有一个前提，就是梯度大的方向对应的 $H$ 的特征值也大，由此可得：只有那些对减小目标函数梯度影响很大的方向的成分才不受正则化影响；那些对梯度下降影响不大的方向，会得到一个较小的特征值，从而使那些不重要方向的成分在训练中一直在缩小。

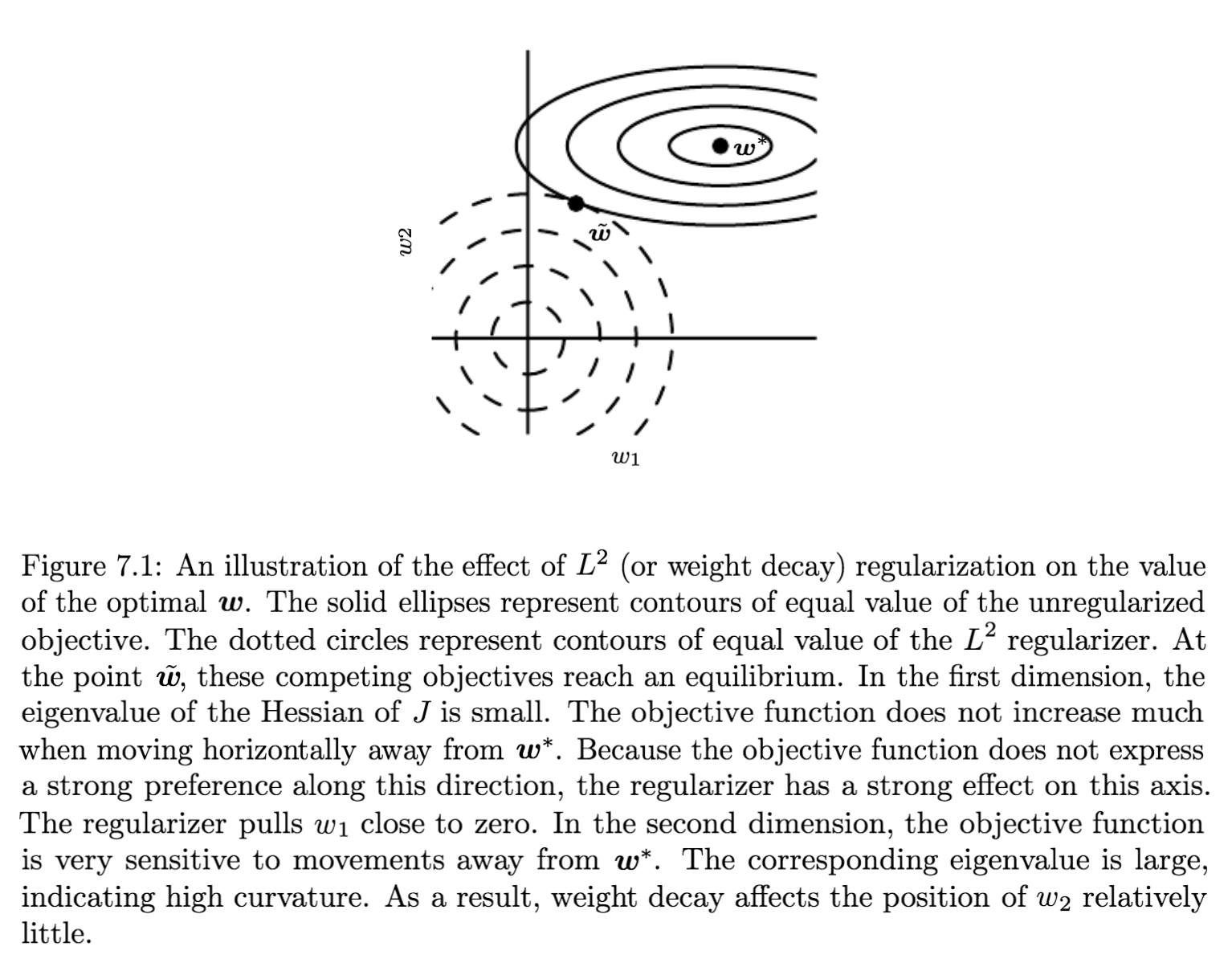
上面我们讨论了泛化的、通用的情况下 $L^2$ 正则化的作用，下面来看一个线性回归的具体实例。线性回归的均方误差目标函数为： \[ (Xw-y)^T(Xw-y) \] 增加 $L^2$ 正则化之后变成： \[ (Xw-y)^T(Xw-y)+\frac{1}{2}\alpha w^Tw \] 解出 $w$ 的正规方程也从 \[ w = (X^TX)^{-1}X^Ty \] 变为： \[ w=(X^TX+\alpha I)^{-1}X^Ty \] 可见，下面的式子只是把 $(X^TX)^{-1}$ 换成了 $(X^TX+\alpha I)^{-1}$，在 $X^TX$ 的对角线上多加了 $\alpha$ 。但是 $X^TX$ 对角线上的元素对应的就是输入特征的方差，也就是$L^2$正则化增加了输入特征的方差，从而迫使模型去降低那些没有用（与输出目标的协方差很低）的特征的权重。

$L^1$ Regularization

对于 $L^1$ 正则化，它的惩罚项就是权重 $w$ 的1范数： \[ \Omega(\theta) = ||w||_1 = \sum_i|w_i| \] 还像上面一样不考虑偏置参数，$\alpha$ 为正则化因子，则使用 $L^1$ 正则化的目标函数为： \[ \hat{J}(w;X,y) = \alpha||w||_1 + J(w;X,y) \] 相应的梯度为： \[ \bigtriangledown_w\hat{J}(w;X,y) = \alpha sign(w) + \bigtriangledown_wJ(w;X,y) \] 其中 $sign$ 为符号函数，大于 $0$ 值为 $1$，小于 $0$ 值为 $-1$，等于 $0$ 值为 $0$ 。

这里可以看出，$L^1$ 正则化不是在按照一定比例来缩小参数 $w$，而是每步增加或减少一个常量。

为了观察整体训练过程中正则化的影响，我们继续用在最优点 $w^*$ 的二次逼近来拟合目标函数： \[ \hat{J}(w) = J(w^*)+\frac{1}{2}(w-w^*)^TH(w-w*) \] 相应的梯度为： \[ \bigtriangledown_w\hat{J}(w) = H(w - w^*) \] 这里的 $H$ 依旧是海森矩阵，由于 $L^1$ 惩罚相不保证可以用一个代数式表示（clean algebraic expression），所以假设 $H$ 是个对角阵，$H = diag([H_{1,1}, …, H_{n,n}])$，并且每个 $H_{i,i} > 0$。只要 Linear Regression 的输入特征直接没有关联（correlation）就可以保证上述假设成立，而这一点可以通过PCA做到。

加上 $L^1$ 正则化的目标函数为： \[ \hat{J}(w;X,y) = J(w^*; X,y) + \sum_i\left[ \frac{1}{2}H_{i,i}(w_i-w^*_i)^2+\alpha|w_i| \right] \] 最小化该目标函数可得： \[ w_i = sign(w^*_i)\max\left\{|w^*_i| - \frac{\alpha}{H_{i,i}}, 0\right\} \] 考虑所有 $w_i^* > 0$，有两种可能结果：

当 $w_i^*≤\frac{\alpha}{H_{i,i}}$ 时，$w_i$ 的最优解为 $0$。This occurs because the contribution of $J(w;X,y)$ to the regularized objective $\hat{J}(w;X,y)$ is overwhelmed—in direction $i$ —by the $L^1$ regularization which pushes the value of $w_i$ to zero.
当 $w_i^*≥\frac{\alpha}{H_{i,i}}$ 时，这是最优的 $w_i$ 不会为 $0$，而是会向 $0$ 的方向移动 $\frac{\alpha}{H_{i,i}}$ 的距离。

当所有 $w^*_1 < 0$ 时也有类似的结果。

和 $L^2$ 正则化相比，$L^1$ 正则化趋向于使权重变的稀疏（sparse），也就是说一部分参数的最优值为 $0$。如果我们用同样的假设分析 $L^2$ 正则化，则会得到 $\hat{w}_i = \frac{H_{i,i}}{H_{i,i}+\alpha}w^*_i$，只要 $w_i^*$ 非零，$\hat{w}_i$ 一定也非零。所以 $L^2$ 正则化不会使参数变稀疏，而 $L^1$ 正则化在 $\alpha$ 很大的情况下会。

$L^1$ 正则化的这个性质可以用来做特征选择（feature selection），如果某个特征对模型收敛帮助不大，则它对应的权重会收缩到 $0$，我们就可以去掉那些用处不大的特征。

Maximum A Posteriori (MAP) Estimation \[ \theta_{MAP} = \arg\max_\theta p(\theta|x) = \arg\max_\theta \log p(x|\theta)+\log p(\theta) \] Maximum Likelihood Estimator (MLE) \[ \theta_{ML} = \arg\max_\theta p(X;\theta) \]

正则化与参数估计之间的关系

使用均方误差的线性回归可以看作是对参数 $w$ （如果 $w$ 的先验服从 $N(w;0,\frac{1}{\lambda}I^2)$）的最大似然估计（MLE），如果加上 $L^2$ 正则化项 $\lambda w^T w$ 的话，则变成了对参数 $w$ 的最大后验估计（MAP），因为： \[ \log p(w) = \log N(w;0,\frac{1}{\lambda}I^2)=\log\frac{\lambda}{\sqrt{2\pi}} - \frac{1}{2}\lambda w^Tw \] 而 $L^1$ 正则化则相当于 $w$ 的先验估计服从各向同性拉普拉斯分布（isotropic Laplace distribution）： \[ \log p(w) = \sum_i\log Laplace(w_i; 0, \frac{1}{\alpha}) = -\alpha ||w||_1 + n\log\alpha -n\log2 \] 我们可以忽略 $n\log\alpha -n\log2$ 因为它们不依赖于 $w$。

Regularization and Under-Constrained Problems

正则化不光可以解决过拟合问题，还可以解决其他很多问题。

比如求解线性回归中，正规方程为 $w = (X^TX)^{-1}X^Ty$，但 $X^TX$ 有可能是不可逆的，比如特征多但样本少的时候， $X^TX$ 就不可逆，这时候如果加上 $L^2$ 正则项，变成 $X^TX+\alpha I$，这可以保证一定是可逆的。

还有一种情况，在 Logistic 回归中，假设数据集是线形可分的，如果参数 $w$ 可以完美的进行分类，那么 $2w$ 一定也可以，而且会有更大的似然。这样循环更新的算法（梯度下降）就会使 $w$ 不断增大，直到发生溢出。而加上正则化可以防止这种情况的发生，比如加上 $L^2$ 正则项，当权重衰减的指数和似然的坡度持平时，就会停止增大参数。（For example, weight decay will cause gradient descent to quit increasing the magnitude of the weights when the slope of the likelihood is equal to the weight decay coeﬃcient.）

再比如求 Moore-Penrose 伪逆： \[ X^+ = \lim_{\alpha\rightarrow0}(X^TX+\alpha I)^{-1}X^T \] 我们现在可以认为上式是在求带 $L2$ 正则项的线性回归，也就可以把它解释为用正则化解决欠问题（underdetermined problems）。

Dataset Augmentation

数据集增强是提高机器学习模型泛化能力的一种方法，主要应用于分类算法中，操作通常包括对输入添加白噪声、对输入进行变换、对神经网络中间添加噪声等，但注意对输入变换时不要改变标签值。这种数据集增强的方法被证明在物体识别和语音识别方面很有作用。

但在比较两个机器学习模型好坏时，一定要在相同的数据集和数据集增强操作的情况下进行比较。

Noise Robustness

Injecting Noise at the Output Targets

因为大多数数据集都包含错误标签，若 $y$ 是错误的则最大化 $\log p(y|x)$ 将会带来很大危害。一个解决办法是给标签添加噪声，比如假设一个小常量 $\epsilon$ ，训练集中 $1-\epsilon$ 的概率的标签是正确的，剩下 $\epsilon$ 概率的标签则不一定。我们不用实际在样本中加入噪声，而是直接把 $\epsilon$ 嵌入到目标函数中。比如 label smoothing 技术把hard target $0$ 和 $1$ 替换成 $\frac{\epsilon}{k-1}$ 和 $1-\epsilon$，标准的交叉熵损失就是为了处理这种 soft target。而事实上，最大似然学习 + softmax + hard target 根本不会收敛，因为 softmax 肯定不会输出绝对地 $0$ 或 $1$。

Multi-Task Learning

多任务学习也是一种提高模型泛化能力的方法，多个任务使用相同的输入，但输出不同，整个模型的参数分为两部分：

任务相关的参数，只从任务相关的样本中优化参数，在下图中的上层
一般的参数，不与任务相关，可以从所有样本中更新参数，在下图中的底层（$h^{(shared)}$）。

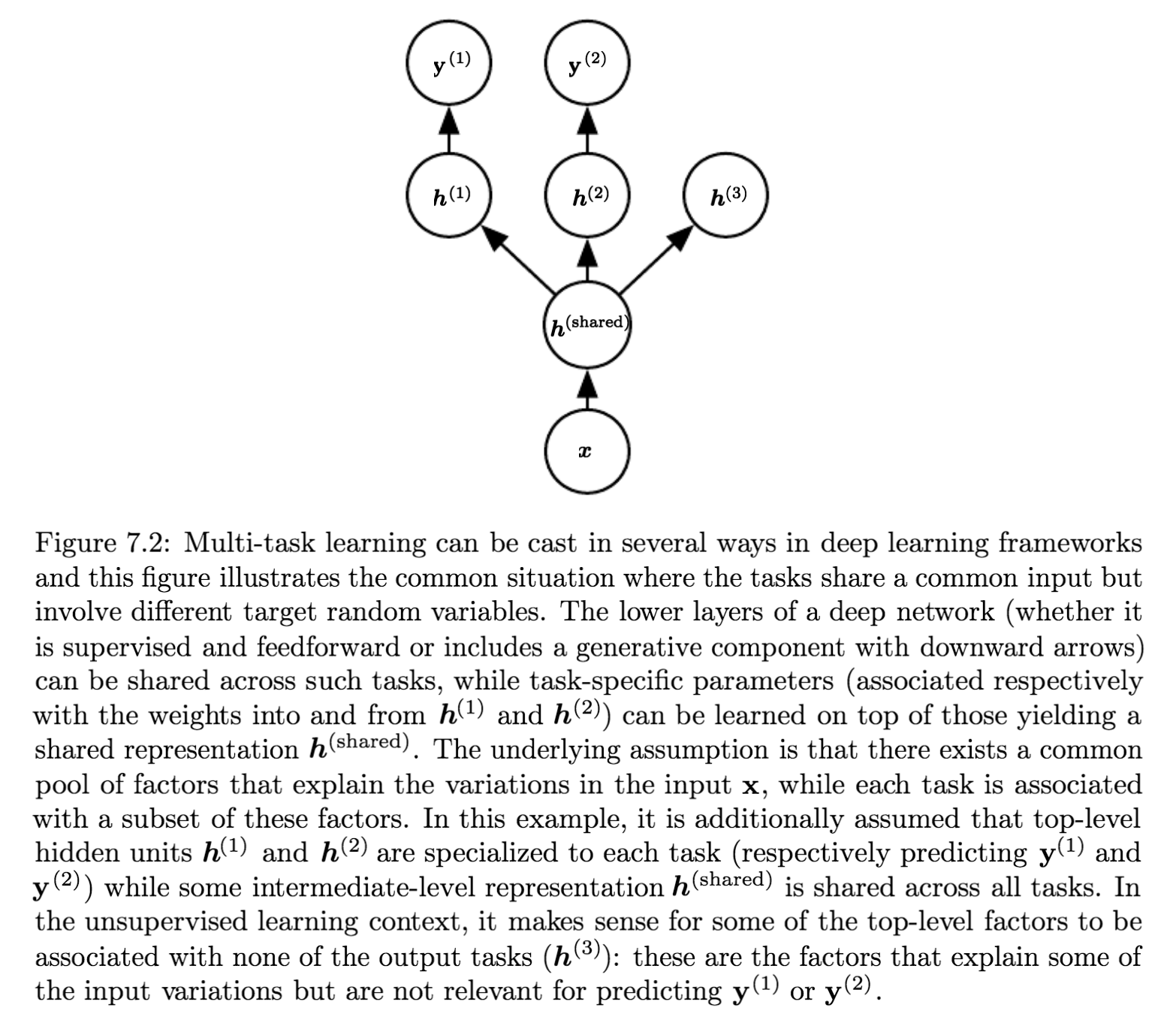
从深度学习的角度来说：among the factors that explain the variations observed in the data associated with the diﬀerent tasks, some are shared across two or more tasks.

Early Stopping

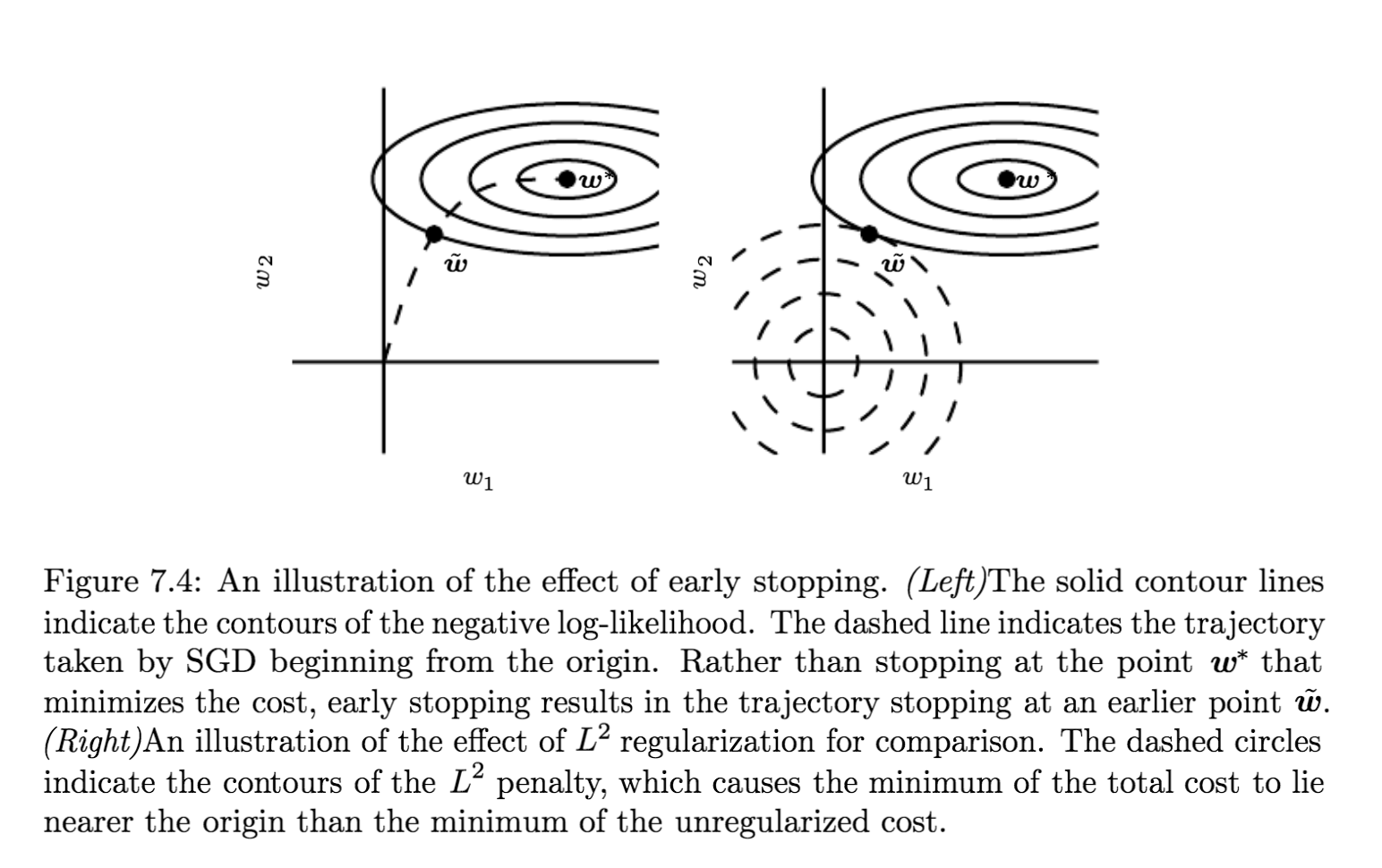
如果我们的机器学习模型拟合能力过强的话，就会发生这种情况，训练误差一直减小，但交叉验证的误差先减小，然后在某个值达到最小，后来又增大，如下图所示。

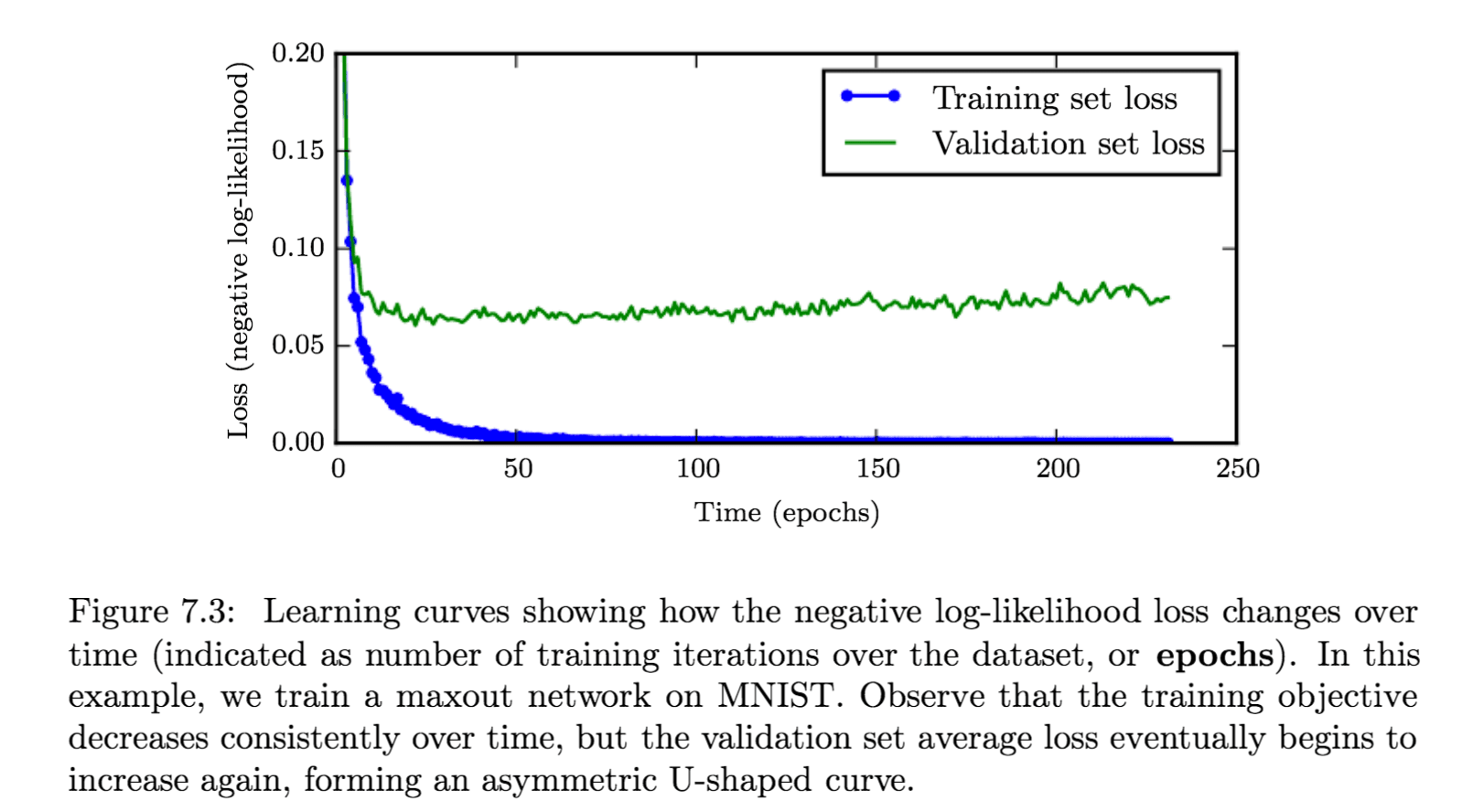
这时我们可以使用 early stopping 策略，在每次计算 validation loss 之后，把该 loss 与达到的最小值比较，若它小于最小值，则更新最小值并拷贝一份当前的参数；否则继续下一轮训练。训练结束返回拷贝的参数而不是最后一轮训练的参数。

Early stopping 策略是一种很常用正则化方法，因为它既有效又简单。它也可以看做是超参数选择的方法，因为训练的轮数也是个超参数，而应用 early stopping 策略就可以自动选择这个值，而不需要大量猜测。

How early stopping acts as a regularizer

Early stopping 会限制权重更新次数，即限制了权重（参数）远离初始权重的距离，如果最佳采取 $\tau$ 轮迭代，学习速率为 $\epsilon$ ，那么它俩的乘积 $\epsilon\tau$ 就类似于 $L^2$ 正则化中的系数！

NIUHE